Question

The following formula for the sum of the cubes of the first n integers is proved. Use it to evaluate the area under the curve y = x³ from 0 to 1 as a limit,

1³ + 2³ + 3³ +...+ n³ = [n(n+1)/2]².

Answer 1

Therefore, area under the curve is
`(1)/(4)`

Explanation:

We have to find the area under curve y = x³ from 0 to 1 as limit.

Since Area 'A' =
`\lim_(n \to \infty) \sum_(i=1)^(n)f(x_(i))\triangle x`

The given function is f(x) = x³

Since
`x_(i)=a+\triangle x.i`

Here a = 0 and
`\triangle x=(1-0)/(n)=(1)/(n)`

`f(x_(i))=((i)/(n))^(3)`

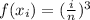
Now A =
`\lim_(n \to \infty) \sum_(i=1)^(n)f(x_(i))\triangle x= \lim_(n \to \infty)\sum_(i=1)^(n)((i)/(n))^(3)((1)/(n))`

`= \lim_(n \to \infty)(1)/(n^(4))\sum_(i=1)^(n)i^(3)`

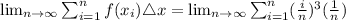
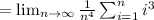
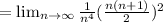`= \lim_(n \to \infty)(1)/(n^(4))( (n(n+1))/(2))^(2)` Since 1³ + 2³ + 3³..............n³ =
`[(n(n+1))/(2)]^(2)`

`= \lim_(n \to \infty)(n^(2)(n+1)^(2))/(4n^(4))`

`= \lim_(n \to \infty)(1)/(4)(1+(1)/(n))^(2)`

`=(1)/(4)(1+0)`

`=(1)/(4)`

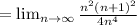
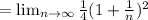
Therefore, area under the curve is
`(1)/(4)`