Question

The campsite shop sells boxes of funshine cereal. The base of each box is a 180mm x 60 mm rectangle. The shelf where the boxes are displayed is a 65 cm x 35 cm rectangle

Answer 1

A maximum of 21 boxes will fit in the shelf.

Explanation:

Question

The campsite shop sells boxes of fun-shine Cereal.

The base of each box is a 180 mm x 60 mm rectangle.

The shelf where the boxes are displayed is a 65 cm x 35 cm rectangle.

Work out the maximum number of boxes that will fit on the shelf.

Given:

Dimension of each rectangle box =
`180\ mm* 60\ mm`

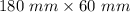
Dimension of the rectangular shelf where the boxes are displayed =
`65\ cm * 35\ cm`

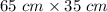
To find the maximum number of boxes that would fit on the shelf.

Solution:

First of all we will convert all units to centimeters.

1 mm = 0.1 cm

Then, 180 mm =
`180\ mm* (0.1\ cm)/(1\ mm)=18\ cm`

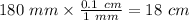
Then, 60 mm =
`60\ mm* (0.1\ cm)/(1\ mm)=6\ cm`

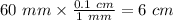
Dimensions of the box in centimeters =
`18\ cm * 6\ cm`

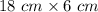
Area of each rectangle box =
`length* width=`
`18\ cm * 6\ cm`
`=108\ cm^2`

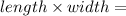
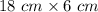
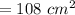
Area of the shelf =
`65\ cm * 35\ cm`
`=2275\ cm^2`

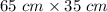
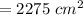
To find the maximum number of boxes that would fit in the shelf, we will dived the area of shelf by the area of each box.

So, maximum number of boxes that would fit in the shelf =
`(2275\ cm^2)/(108\ cm^2)=21.06\approx 21`

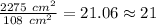
Thus, a maximum of 21 boxes will fit in the shelf.