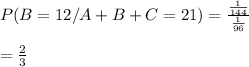Answer:
a) 0.73684
b) 2/3
Explanation:
part a)
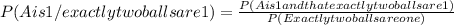
Using conditional probability as above:
(A,B,C)
Cases for numerator when:
P( A is 1 and exactly two balls are 1) = P( 1, not 1, 1) + P(1, 1, not 1)
=
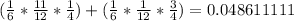
Cases for denominator when:
P( Exactly two balls are 1) = P( 1, not 1, 1) + P(1, 1, not 1) + P(not 1, 1 , 1)

Hence,
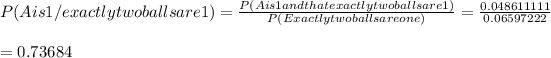
Part b
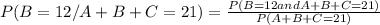
Cases for denominator when:
P ( A + B + C = 21) = P(5,12,4) + P(6,11,4) + P(6,12,3)
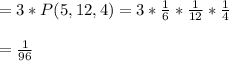
Cases for numerator when:
P (B = 12 & A + B + C = 21) = P(5,12,4) + P(6,12,3)
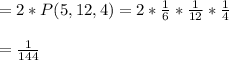
Hence,