Question

Determine all real values of p such that the set of all linear combination of u = (3, p) and v = (1, 2) is all of R2. Justify your answer.

Answer 1

p ∈ IR - {6}

Explanation:

The set of all linear combination of two vectors ''u'' and ''v'' that belong to R2

is all R2 ⇔

`u\\eq 0_(R2)`

`v\\eq 0_(R2)`

And also u and v must be linearly independent.

In order to achieve the final condition, we can make a matrix that belongs to
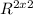`R^(2x2)` using the vectors ''u'' and ''v'' to form its columns, and next calculate the determinant. Finally, we will need that this determinant must be different to zero.

Let's make the matrix :

`A=\left[\begin{array}{cc}3&1&p&2\end{array}\right]`

We used the first vector ''u'' as the first column of the matrix A

We used the second vector ''v'' as the second column of the matrix A

The determinant of the matrix ''A'' is

`Det(A)=6-p`

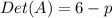
We need this determinant to be different to zero

`6-p\\eq 0`

`p\\eq 6`

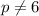
The only restriction in order to the set of all linear combination of ''u'' and ''v'' to be R2 is that
`p\\eq 6`

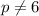
We can write : p ∈ IR - {6}

Notice that is
`p=6` ⇒

`u=(3,6)`

`v=(1,2)`

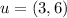
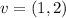
If we write
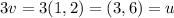`3v=3(1,2)=(3,6)=u` , the vectors ''u'' and ''v'' wouldn't be linearly independent and therefore the set of all linear combination of ''u'' and ''b'' wouldn't be R2.