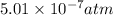Question

Consider this reaction occurring at 298 K:

N2O(g) + NO2(g) ⇆ 3 NO(g)

If a reaction mixture contains only N2O and NO2 at partial pressures of 1.0 atm each, the reaction will be spontaneous until some NO forms in the mixture.
What maximum partial pressure of NO builds up before the reaction ceases to be spontaneous?

Answer 1

The question is incomplete, here is the complete question:

Consider this reaction occurring at 298 K:

`N_2O(g)+NO_2(g)\rightleftharpoons 3NO(g)`

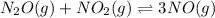
If a reaction mixture contains only
`N_2O\text{ and }NO_2` at partial pressures of 1.0 atm each, the reaction will be spontaneous until some NO forms in the mixture.

What maximum partial pressure of NO builds up before the reaction ceases to be spontaneous. Given that:
`\Delta G^o_(rxn)=107.8kJ/mol`

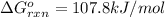
Answer: The maximum partial pressure of NO will be
`5.01* 10^(-7)atm`

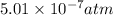
Step-by-step explanation:

For the given chemical equation:

`N_2O(g)+NO_2(g)\rightleftharpoons 3NO(g)`

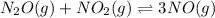
The expression of
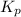`K_p` for above equation follows:

`K_p=(p_(NO)^3)/(p_(N_2O)* p_(NO_2))`

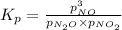
When the reaction ceases to be spontaneous, the
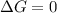`\Delta G=0` (at equilibrium)

Relation between standard Gibbs free energy and equilibrium constant follows:

`\Delta G=\Delta G^o+2.303RT\log K_p`

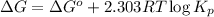
where,

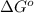`\Delta G^o` = Standard Gibbs free energy = 107.8 kJ/mol = 107800 J/mol (Conversion factor: 1 kJ = 1000 J )

R = Gas constant =
`8.314J/K mol`

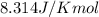
T = temperature = 298 K

`p_(N_2O)=1.00atm`

`p_(NO_2)=1.00atm`

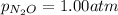
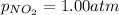
Putting values in above equation, we get:

`0=107800J/mol+(2.303* 8.314J/Kmol)* 298K* \log ((p_(NO)^3)/(1.00* 1.00))`

`-107800=5705.85* \log ((p_(NO)^3)/(1.00* 1.00))\\\\-18.893=\log (p_(NO)^3)-\log (1.00)\\\\-18.893=3\log (p_(NO))\\\\\log (p_(NO))=-6.30\\\\p_(NO)=10^(-6.30)=5.01* 10^(-7)atm`

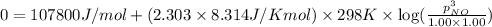
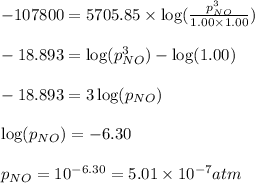
Hence, the maximum partial pressure of NO will be
`5.01* 10^(-7)atm`