Answer:
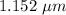

Step-by-step explanation:
d = Gap between slits = 0.142 mm
 = Wavelength of light = 576 nm
= Wavelength of light = 576 nm
L = Distance between light and screen = 3.5 m
m = Order = 2
Difference in path length is given by
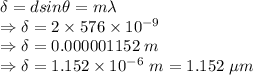
The difference in path lengths is
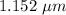
For dark fringe the difference in path length is given by
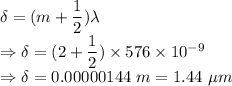
The difference in path length is
