Question

Consider an airplane modeled after the twin-engine Beechcraft Queen Air executive transport. The airplane has the following characteristics: weight is 38,220 N; wing area is 27.3 m2; aspect ratio is 7.5; Oswald efficiency factor is 0.9; and zero-lift drag coefficient CD,0 is 0.03.

1) Calculate the thrust required to fly at a velocity of 725 km/h at standard sea level. Assume the value of ?? = 1.225 kg/m3 at standard sea level. (Round the final answer to the nearest whole number.) The thrust required to fly at a velocity of 725 km/h at standard sea level is _______N.
2) Calculate the thrust required to fly with a velocity of 725 km/h at an altitude of 4.5 km. Assume the value of ?? = 0.777 kg/m3 at an altitude of 4.5 km. (Round the final answer to the nearest whole number.) The thrust required to fly with a velocity of 725 km/h at an altitude of 4.5 km is _______ N.

Answer 1

(A) 3052.7 N

(B)13,089.1 N

Step-by-step explanation:

weight (w) = 38,220 N

wing area (A) = 27.3 m^{2}

Oswald efficiency factor (E) = 0.9

zero-lift drag coefficient (CD0) = 0.03

velocity (v) = 725 km/h = 201.4 m/s

density of air (p) = 1.225 kg/m^{3}

aspect ratio (AR) = 7.5

(A) at standard sea level

weight (w) =
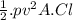`(1)/(2).pv^(2) A.Cl` where Cl = lift coefficient

Cl =
`(2w)/(pAv^(2) )`=
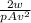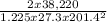`(2x38,220)/(1.225x27.3x201.4^(2) )` = 0.5635

coefficient of drag (Cd) = CDO +
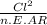`(Cl^(2) )/(n.E.AR)` (take note that π is shown as
`n`)

Cd = 0.03 +
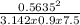`(0.5635^(2) )/(3.142x0.9x7.5)` = 0.045

Cl/Cd = L/D (lift to drag ratio) = 0.5635/0.045 =12.52

Thrust required = w/(l/d) = 38220 / 12.52 = 3052.7 N

(B) At altitude of 4.5 km

density (p) = 0.777 kg/m^{3}

Cl =
`(2w)/(pAv^(2) )`=
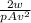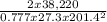`(2x38,220)/(0.777x27.3x201.4^(2) )` = 0.0888

coefficient of drag (Cd) = CDO +
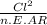`(Cl^(2) )/(n.E.AR)` (take note that π is shown as
`n`)

Cd = 0.03 +
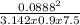`(0.0888^(2) )/(3.142x0.9x7.5)` = 0.0304

Cl/Cd = L/D (lift to drag ratio) = 0.0888/0.0304 =2.92

Thrust required = w/(l/d) = 38220 / 2.92 = 13,089.1 N