Question

Entalpy of vaporization of water is 41.1k/mol. if the vapor pressure of water at 373k is 101.3 kpa, what is the vapor pressure of water at 298k?

Answer 1

Answer: The vapor pressure of water at 298 K is 3.565kPa.

Step-by-step explanation:

The vapor pressure is determined by Clausius Clapeyron equation:

`ln((P_2)/(P_1))=(\Delta H_(vap))/(R)((1)/(T_1)-(1)/(T_2))`

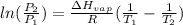
where,

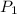`P_1` = initial pressure at 298 K = ?

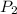`P_2` = final pressure at 373 K = 101.3 kPa

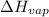`\Delta H_(vap)` = enthalpy of vaporisation = 41.1 kJ/mol = 41100 J/mol

R = gas constant = 8.314 J/mole.K

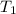`T_1` = initial temperature = 298 K

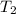`T_2` = final temperature = 373 K

Now put all the given values in this formula, we get

`\log ((101.3)/(P_1))=(41100)/(2.303* 8.314J/mole.K)[(1)/(298K)-(1)/(373K)]`

`(101.3)/(P_1)=antilog(1.448)`

`P_1=3.565kPa`

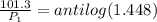
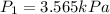
Therefore, the vapor pressure of water at 298 K is 3.565kPa.