Question

Find the appropriate percentile from a​ t-distribution for constructing the following confidence interval.

99​% ​t-interval with n = 3.

Answer 1

Answer: 9.9248

Explanation:

We know that the critical t- value for confidence interval is a two-tailed value from the t-distribution table corresponding to degree of freedom (df = n-1 , where n is the sample size) and the significance level (
`\alpha/2`) .

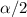The given confidence interval = 99%

⇒ Significance level =
`\alpha=100\%-99\%=1\%=0.01`

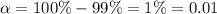
Sample size : n=3

DEgree of freedom : df = n-1 = 2

Then, the critical t- value for 99% confidence interval will be;

`t_(\alpha/2, df)=t_(0.01/2,\ 2)`

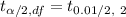
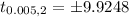`t_(0.005 , 2)=\pm9.9248` [From t-distribution table]

Hence, the appropriate percentile from a​ t-distribution for constructing the 99​% confidence interval with n = 3 is 9.9248.