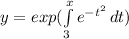Question

Find an explicit solution of the given initial-value problem.dy/dx = ye^x^2, y(3) = 1.

Answer 1

`y=exp(\int\limits^x_4 {e^{-t^(2) } } \, dt)`

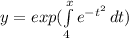
Explanation:

This is a separable equation with an initial value i.e. y(3)=1.

Take y from right hand side and divide to left hand side ;Take dx from left hand side and multiply to right hand side:

`(dy)/(y) =e^{-x^(2) }dx`

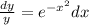
Take t as a dummy variable, integrate both sides with respect to "t" and substituting x=t (e.g. dx=dt):

`\int\limits^x_3 {(1)/(y) } \, (dy)/(dt) dt=\int\limits^x_3 {e^{-t^(2) } } dt`

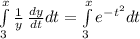
Integrate on both sides:

`ln(y(t))\left \{ {{t=x} \atop {t=3}} \right. =\int\limits^x_3 {e^{-t^(2) } } \, dt`

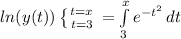
Use initial condition i.e. y(3) = 1:

`ln(y(x))-(ln1)=\int\limits^x_3 {e^{-t^(2) } } \, dt\\ln(y(x))=\int\limits^x_3 {e^{-t^(2) } } \, dt\\`

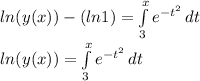
Taking exponents on both sides to remove "ln":

`y=exp (\int\limits^x_3 {e^{-t^(2) } } \, dt)`