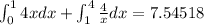Question

Find the area of the region in the first quadrant bounded by the line yequals4​x, the line xequals4​, the curve yequalsStartFraction 4 Over x EndFraction ​, and the​ x-axis.

Answer 1

Explanation:

First of all you need to sketch the region you are looking here. The sketch is in the attachment.

This area can be separated into two. The one below the line defined by
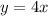`y=4x` and one below the curve
`y=(4)/(x)`

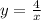
After that you should find the point of intersection of the two curves so that integral limits can be defined. This is done by equating the two expressions.

`4x=(4)/(x)\\4x^2=4\\x^2=1\\x=\pm1`

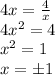
So the first integral has the limits
`x=0` and
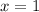`x=1\\`, while the second one is defined with
`x=1` and the limit
`x=4`.

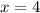You now just add the two integrals and that's your area:

`\int_0^14xdx + \int_1^4(4)/(x)dx=7.54518`