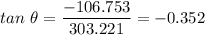Question

A plane leaves the airport in Galisteo and flies 160 km at 66.0 ∘ east of north; then it changes direction to fly 260 km at 49.0 ∘ south of east, after which it makes an immediate emergency landing in a pasture?

Answer 1

The question doesn't have any particular requirement, but we'll compute the displacement of the plane from its initial and final landing point in the pasture

Answer:

`\displaystyle |\vec{r}|=321.464\ km`

`\displaystyle \theta =-19.395^o`

Step-by-step explanation:

Displacement

The vector displacement
`\vec r` is a measure of the change of position of a moving object. The displacement doesn't depend on the path followed, only on the final and initial positions. Its scalar counterpart, the distance, does measure the total space traveled and considers all the changes in the direction taken by the object. To find the displacement, we must add all the particular displacements by using vectors.

The plane first flies 160 km at 66° east of north. To find the vector expression of this displacement, we must know the angle with respect to the East direction or North of East. Knowing the angle East of North is 66°, the required angle is 90°-66°=34°

The first vector is expressed as

`\displaystyle \vec{r_1}=\left \langle 160^o\ cos34^o, 160\ sin34^o \right \rangle`

`\displaystyle \vec{r_1}=\left \langle 132.646, 89.471 \right \rangle`

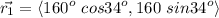
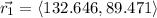
The second displacement is 260 km at 49° South of East. This angle is below the horizontal respect to the reference, thus we use -49°.

The second vector is expressed as:

`\displaystyle \vec{r_2}=\left \langle 260\ cos(-49^o), 260\ sin(-49^o)\right \rangle`

`\displaystyle \vec{r_2}=\left \langle 170.575,-196.224\right \rangle`

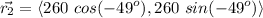
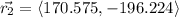
The total displacement is computed as the vectorial sum of both vectors

`\displaystyle \vec{r}=\vec{r_1}+\vec{r_2}=\left \langle 132.646+170.575\right \rangle+ \left \langle89.471-196.224\right \rangle`

`\displaystyle \vec{r}=\left \langle 303.221,-106.753\right \rangle\ km`

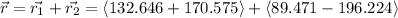
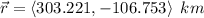
The magnitude of the total displacement is

`\displaystyle |\vec{r}|=√(303.221^2+(-106,753)^2)`

`\displaystyle |\vec{r}|=321.464\ km`

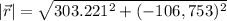
And the direction is

`\displaystyle tan\ \theta =(-106.753)/(303.221)=-0.352`

`\displaystyle \theta =-19.395^o`