Question

A helicopter leaves bristol and flies due east for 10 miles.Then the helicopter flies 8miles north before landing. What is the direct distance of the helicopter from bristol?

Answer 1

The distance of the helicopter from the bristol is approximately 12.81 miles

Explanation:

Given:

Helicopter flies 10 miles east of bristol.

Then the helicopter flies 8 miles North before landing.

To find the direct distance between the helicopter and bristol.

Solution:

In order to find the distance of the helicopter from the bristol before landing, we will trace the path of the helicopter

The helicopter is first heading 10 miles east of bristol and then going 8 miles due north.

On tracing the path of the helicopter we find that the direct distance of the helicopter from the bristol is the hypotenuse of a right triangle formed by enclosing the path of the helicopter.

Applying Pythagorean theorem to find the hypotenuse of the triangle.

`Hypotenuse^2=Short\ leg^2+Shortest\ leg^2`

`Hypotenuse^2=10^2+8^2`

`Hypotenuse^2=100+64\\Hypotenuse^2=164`

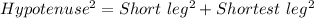
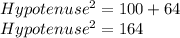
Taking square root both sides.

`√(Hyptenuse^2)=√(164)\\Hypotenuse = 12.81\ miles`

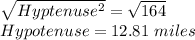
Thus, the distance of the helicopter from the bristol is approximately 12.81 miles