Answer:
q=0.06 C
Step-by-step explanation:
Given that
Net flux
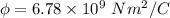
Lets take charge inside Gaussian surface = q C
We know that
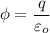
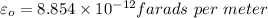
Now by putting the values in the above equation we get
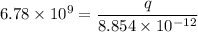
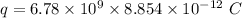
q=0.06 C
Therefore the net charge inside the surface will be 0.06 C.
q=0.06 C