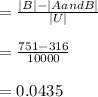Question

Human visual inspection of solder joints on printed circuit boards can be very subjective. Part of the problem stems from the numerous types of solder defects (e.g., pad non-wetting, knee visibility, voids) and even the degree to which a joint possesses one or more of these defects. Consequently, even highly trained inspectors can disagree on the disposition of a particular joint. In one batch of 10,000 joints, inspector A found 728 that were judged defective, inspector B found 744 such joints, and 1365 of the joints were judged defective by at least one of the inspectors. Suppose that one of the 10,000 joints is randomly selected.a. What is the probability that the selected joint was judged to be defective by neither of the two inspectors?b. What is the probability that the selected joint was judged to be defective by inspector B but not by inspector A?

Answer 1

a) 0.8841

b) 0.0435

Explanation:

A : the set of joints deemed defective by inspector A.

B: the set of joints deemed defective by inspector B.

U: the set of all joints.

The problem says |A|=724, |B|=751, |A∪B|=1159, |U|=10000. Hence, with the help of Venn diagram we can answer the following:

Part a)

This asks for the number of joints that are ∉(A∪B).

hence,

P (∉(A∪B)) :

`(10000-1159)/(10000) \\\\=0.8841`

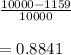
part b)

This asks for the number of joints that are in B but not in A, which Is represented as the set B−A

`= (|B| - |AandB| )/(|U|)\\\\= (751-316 )/(10000)\\\\= 0.0435`