Question

Assume that at sea-level the air pressure is 1.0 atm and the air density is 1.3 kg/m3.

(a) What would be the height of the atmosphere if the air density were constant?
km

(b) What would be the height of the atmosphere if the air density decreased linearly to zero with height?

Answer 1

Pressure, P = 1 atm

air density, ρ = 1.3 kg/m³

a) height of the atmosphere when the density is constant

Pressure at sea level = 1 atm = 101300 Pa

we know

P = ρ g h

`h = (P)/(\rho\ g)`

`h = (101300)/(1.3* 9.8)`

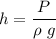
h = 7951.33 m

height of the atmosphere will be equal to 7951.33 m

b) when air density decreased linearly to zero.

at x = 0 air density = 0

at x= h ρ_l = ρ_sl

assuming density is zero at x - distance

`\rho_x = (\rho_(sl))/(h)* x`

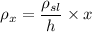
now, Pressure at depth x

`dP = \rho_x g dx`

`dP = (\rho_(sl))/(h)* x g dx`

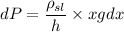
integrating both side

`P = g(\rho_(sl))/(h)* \int_0^h x dx`

`P =(\rho_(sl)* g h)/(2)`

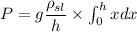
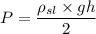
now,

`h=(2P)/(\rho_(sl)* g)`

`h=(2* 101300)/(1.3* 9.8)`

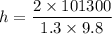
h = 15902.67 m

height of the atmosphere is equal to 15902.67 m.