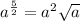Answer:
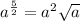
Explanation:
Given:
Given expression is.

We need to write the given expression in radical form.
Solution:
Rewrite the expression as.

Now we extract power as

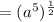
Now we write the above expression in radical form and simplify.
![=\sqrt[2]{(a^(5))}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jy8ijg5awg9lp6pmdn18r0vbox374elnuq.png)
![=\sqrt[2]{(a* a)* (a* a)* a}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/oqii4esiepc09dbwy2mjnpxa2l4je4uke4.png)
![=\sqrt[2]{a^(2)* a^(2)* a }](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ot4v1blsp2sr8b7x8n7i40r1e0jbns9y9w.png)
![= a* a* \sqrt[2]{a}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7603vxx2kr40t6kklklq9bra3duay6im8v.png)
![= a^(2)* \sqrt[2]{a}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/5xoavoxymltiylsuupudq97zji9w89hxe7.png)
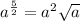
Therefore, the radical form of the given expression