Question

Working alone at its own constant rate, a machine seals k cartons in 8 hours, and working alone at its own constant rate, a second machine seals k cartons in 4 hours. If the two machines, each working at its own constant rate and for the same period of time, together sealed a certain number of cartons, what percent of the cartons were sealed by the machine working at the faster rate?A. 25%B. 3313%C. 50%D. 6623%E. 75%

Answer 1

`66(2)/(3)\%`

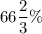
Explanation:

Given,

The number of cartons = k,

Time taken by machine a = 8 hours,

So, the number of cartons made by machine a in one hour

=
`\frac{\text{Cartons in 8 hours}}{8}`

=
`(k)/(8)`

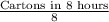
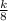
Time taken by machine b = 4 hours ,

So, the number of cartons made by machine b in one hour

=
`(k)/(4)`

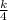
Total cartons made in 1 hour =
`(k)/(8)+(k)/(4)`

`=(k+2k)/(8)`

`=(3k)/(8)`

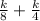
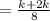
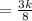
∵ for the whole number value of k,

`(k)/(4)>(k)/(8)`

i.e. machine b is faster,

Also, the percent of the cartons were sealed by the machine b

`=\frac{\text{Cartons made in 1 hour by machine b}}{\text{Total cartons}}* 100`

`=((k)/(4))/((3k)/(8))* 100`

`=(2)/(3)* 100`

`=(200)/(3)`

`=66(2)/(3)\%`

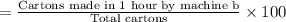
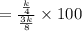
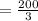
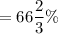
Hence, OPTION D is correct.