Question

Between 1911 in 1990, the top of the leaning bell tower of Pisa, Italy moved toward the south at an average rate of 1.2 MM/Y. The tower is 55M tall. In radians per second, what is the average regular speed of the towers top about its base?

Answer 1

Angular speed of the towers top about its base is
`6.91* 10^(-13)` rad per sec.

Explanation:

Linear velocity of leaning bell tower 'v' = 1.2 mm per year

v =
`(1.2* 10^(-3))/(365* 24* 60* 60)`

v = 3.8 ×
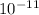`10^(-11)` meter per second

Height of the tower = 55 meter

From the formula of angular velocity,

v = rω

ω =
`(v)/(r)`

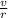
ω =
`(3.8* 10^(-11))/(55)`

ω =
`6.91* 10^(-13)` rad per second.

Therefore, top of the tower is moving with an angular speed of
`6.91* 10^(-13)` rad per second.