Answer:
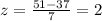
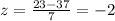
So then as we can see we want the probability that the values would be within 2 deviations from the mean. And from the empirical rule we know that within two deviation from the mean we have at least 95% of the data.
So then we can answer this question like this:
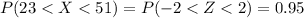
Or 95%
Step-by-step explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ). Broken down, the empirical rule shows that 68% falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
For this case we know that the the random variable X represent the number of phone calls answered by each of the 12 receptionists is bell shaped with a mean
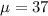 and a standard deviation of
and a standard deviation of
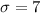 .
.
And for this case we want to find this probability:
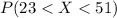
And the best way to solve this is using the z score formula given by:
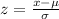
Because the z score quantifies how many deviation we are from the mean.
For the value fo 51 we have this:
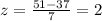
And for the 23 we got:
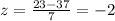
So then as we can see we want the probability that the values would be within 2 deviations from the mean. And from the empirical rule we know that within two deviation from the mean we have at least 95% of the data.
So then we can answer this question like this:
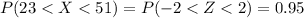
Or 95%