The height of wall of play structure is 8.48 feet
Solution:
A climbing wall leaning against the top of a play structure forms a right triangle with the ground
The figure is attached below
ABC is a right angled triangle
AB is the height of wall of play structure
Let "x" be the height of wall of play structure
AB = x
BC is distance from the bottom of the climbing wall to the base of the play structure
BC = 7 feet
AC is the length of climbing wall
AC = 11 feet
We can apply pythogoras theorem for right angled triangle
Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.
Therefore, by above definition for right angled triangle ABC,
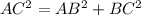
Substituting the values we get,

Thus the height of wall of play structure is 8.48 feet