Question

What is the answer to 3 1/4 cans of red paint and 3 2/12 cans of yellow paint add up to how many cans of orange paint? I know it is 6 cans of orange paint, but don't know the fraction.

Answer 1

The number of orange cans of paint is 6

Solution:

Given that,

`\text{Number of cans of red paint } = 3(1)/(4)\\\\\text{Number of cans of yellow paint } = 3(2)/(12)`

Let us convert the mixed fractions to improper fractions

Multiply the whole number part by the fraction's denominator.

Add that to the numerator.

Then write the result on top of the denominator

`\rightarrow 3(1)/(4) = (4 * 3 + 1)/(4) = (13)/(4)\\\\\rightarrow 3(2)/(12) = (12 * 3 + 2)/(12) = (38)/(12)`

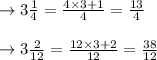
Now we have to add red cans of paint and yellow cans of paint to get orange cans of paint

`\text{Number of cans of orange paint } = (13)/(4) + (38)/(12)`

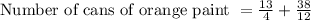
Take L.C.M for denominators

The prime factors of 4 = 2 x 2

The prime factors of 12 = 2 x 2 x 3

For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.

The new superset list is

2, 2, 3

Multiply these factors together to find the LCM.

LCM = 2 x 2 x 3 = 12

`\text{Number of cans of orange paint } = (13)/(4) + (38)/(12)`

`\text{Number of cans of orange paint } = (13 * 3)/(4 * 3) + (38)/(12)\\\\\text{Number of cans of orange paint } = (39)/(12) + (38)/(12)\\\\\text{Number of cans of orange paint } = (77)/(12) = 6.4 \approx 6`

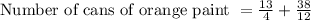
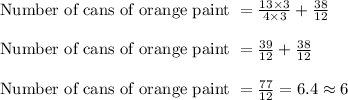
Thus the number of orange cans of paint is 6