Answer:
See proof below.
Explanation:
If we assume the following linear model:

And if we have n sets of paired observations
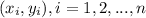 the model can be written like this:
the model can be written like this:
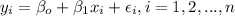
And using the least squares procedure gives to us the following least squares estimates
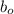 for
for
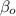 and
and
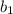 for
for
 :
:
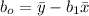
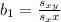
Where:
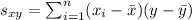
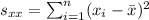
Then
 is a random variable and the estimated value is
is a random variable and the estimated value is
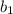 . We can express this estimator like this:
. We can express this estimator like this:
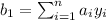
Where
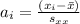 and if we see careful we notice that
and if we see careful we notice that
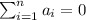 and
and
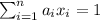
So then when we find the expected value we got:
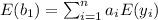
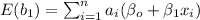
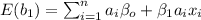
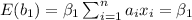
And as we can see
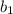 is an unbiased estimator for
is an unbiased estimator for

In order to find the variance for the estimator
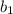 we have this:
we have this:
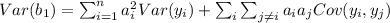
And we can assume that
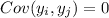 since the observations are assumed independent, then we have this:
since the observations are assumed independent, then we have this:
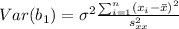
And if we simplify we got:
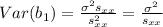
And with this we complete the proof required.