Question

Triangle A B C is shown. The length of A B is 12, the length of B C is 24, and the length of C A is 12 StartRoot 3 EndRoot What are the angle measures of triangle ABC? m∠A = 30°, m∠B = 60°, m∠C = 90° m∠A = 90°, m∠B = 60°, m∠C = 30° m∠A = 60°, m∠B = 90°, m∠C = 30° m∠A = 90°, m∠B = 30°, m∠C = 60°

Answer 1

m∠A = 90°, m∠B = 60°, m∠C = 30°

Explanation:

step 1

see the attached figure to better understand the problem

In this problem we have a right triangle, because the Pythagorean Theorem is satisfied

so

`BC^2=AB^2+AC^2`

`24^2=12^2+(12√(3)) ^2\\\\576=576`

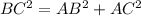
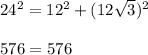
therefore

`m\angle A=90^o`

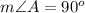
step 2

Find the measure of angle B

we know that

In the right triangle ABC

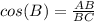`cos(B)=(AB)/(BC)` ----> by CAH (adjacent side divided by the hypotenuse)

substitute the given values

`cos(B)=(12)/(24)`

`m\angle B=cos^(-1)((12)/(24))=60^o`

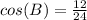
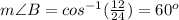
step 3

Find the measure of angle C

we know that

`m\angle B+m\angle C=90^o` ----> by complementary angles

we have

`m\angle B=60^o`

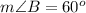
substitute

`60^o+m\angle C=90^o\\m\angle C=30^o`

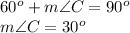
therefore

m∠A = 90°, m∠B = 60°, m∠C = 30°