Question

In a simple model of the hydrogen atom, the electron moves in a circular orbit of radius 0.053nm around a stationary proton.How many revolutions per second does the electron make? Hint: What must be true for a force that causes circular motion?Ans: ___ Hz

Answer 1

Frequency,
`f=6.57* 10^(15)\ Hz`

Step-by-step explanation:

It is given that, the electron moves in a circular orbit of radius 0.053 nm around a stationary proton. The electric force acting on the electron is balanced by the centripetal force as :

`(kq^2)/(r^2)=(mv^2)/(r)`

v is the speed of electron

`v=\sqrt{(ke^2)/(mr)}`

`v=\sqrt{(9* 10^9* (1.6* 10^(-19))^2)/(9.1* 10^(-31)* 0.053* 10^(-9))}`

`v=2.18* 10^6\ m/s`

The speed of electron is given by :

`v=(2\pi r)/(t)`

`t=(2\pi r)/(v)`

`t=(2\pi * 0.053* 10^(-9))/(2.18* 10^6)`

`t=1.52* 10^(-16)\ s`

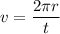
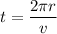
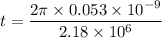
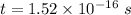
We know that the number of revolutions per second is called frequency of electron. It is given by :

`f=(1)/(t)`

`f=(1)/(1.52* 10^(-16))`

`f=6.57* 10^(15)\ Hz`

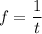
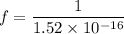
So, the total number of revolutions per second make by the electron is
`f=6.57* 10^(15)\ Hz`. Hence, this is required solution.