Answer:
The solution is the area oh APQ towards the x axis's positive direction as per the image.
Explanation:
We need to graph
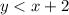 and
and
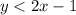 .
.
First, lets find the solution of y < x + 2.
We need to draw the equation of y = x + 2.
If x = 0, y = 2.
If x = 1, y = 3.
Hence, the line y = x + 2 passes through (0, 2) and (1, 3).
The origin (0, 0) satisfies the inequality y < x + 2. Hence, the arrows will be towards the origin.
Now we need to find the solution of y < 2x - 1.
In order to find the solution, we need to draw the equation of the straight line y = 2x - 1.
x = 0 gives y = -1 & x = 1 gives y = 1.
Hence, the equation passes through (0, -1) and (1, 1).
Again (0, 0) does not satisfies the inequality y < 2x - 1, so the arrows for this inequality will be other direction than the origin.