Question

The points (1, r) and (4, -13) lie on a line with slope – 3. Find the missing coordinate r.

Answer 1

The value of missing coordinate "r" is -4

Solution:

Given that,

The points (1, r) and (4, -13) lie on a line with slope – 3

To find: missing coordinate r

The slope of a line is given by formula:

`m = (y_2-y_1)/(x_2-x_1)`

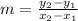
Where, "m" is the slope of line

Here in this sum,

m = -3

`(x_1, y_1) = (1, r)\\\\(x_2, y_2) = (4, -13)`

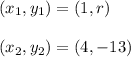
Substituting the values in formula,

`-3 = (-13-r)/(4-1)\\\\-3=(-13-r)/(3)\\\\-9 = -13 - r\\\\r = -13+9\\\\r = -4`

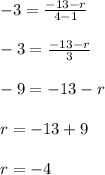
Thus the value of missing coordinate "r" is -4