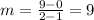Answer:
a. [1,2]
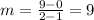
b. [1,3.5]

c. [1,5]
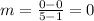
d. [0,3.5]
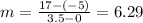
So then we can conclude that the highest slope is for the interval [1,2] and that would be our solution for the fastest average rate.
a. [1,2]
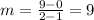
Explanation:
Assuming that we have the figure attached for the function. For this case we just need to quantify the slope given by:
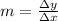
For each interval and the greatest slope would be the interval on which the volume of the box is changing at the fastest average rate
a. [1,2]
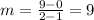
b. [1,3.5]

c. [1,5]
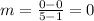
d. [0,3.5]
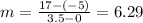
So then we can conclude that the highest slope is for the interval [1,2] and that would be our solution for the fastest average rate.
a. [1,2]