Answer:
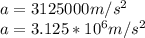
Acceleration, in m/s, of such a rock fragment =
Step-by-step explanation:
According to Newton's Third Equation of motion

Where:
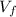 is the final velocity
is the final velocity
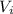 is the initial velocity
is the initial velocity
a is the acceleration
s is the distance
In our case:
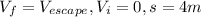
So Equation will become:
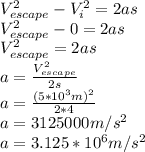
Acceleration, in m/s, of such a rock fragment =