Question

a bacteria population starts with 200 bacteriaa and grows at a rate of r(t) = (450.268)e 1.12567t bacteria per hour. How many bacteria will there be after three hours?

Answer 1

11,513

Step-by-step explanation:

Data provided in the question:

Initial bacteria = 200

Growth rate r(t) =
`(450.268)e^(1.12567t)`

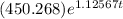
Now,

Total growth after 3 hours =
`\int\limits^3_0 {(450.268)e^(1.12567t)} \, dt`

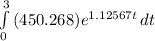
or

Total growth after 3 hours =
`450.268\int\limits^3_0 {e^(1.12567t)} \, dt`

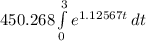
or

Total growth after 3 hours =
`450.268[(e^(1.12567t))/(1.12567)]^3_0`

[ ∵
`\int{d(e^x)}{dt}=(e^x)/((dx)/(dt))`]

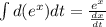Thus,

Total growth after 3 hours = 400 ×
`[{e^(1.12567t)]^3_0`

or

Total growth after 3 hours = 400 ×
`[{e^(1.12567(3))-e^(1.12567(0))]`

or

Total growth after 3 hours ≈ 11313

Hence,

Total bacteria after 3 hours = Initial bacteria + Total growth after 3 hours

= 200 + 11313

= 11,513