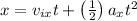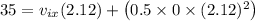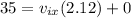Question

1A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

Answer 1

The initial horizontal velocity of the soccer ball is 16.5 m/s

Step-by-step explanation:

When we throw a ball, there is a constant velocity horizontal motion and there is an accelerated vertical motion. These components act independently of each other. Horizontal motion is constant velocity motion.

`v_(x f)=v_(x i)=v_(x)`

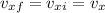
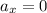`a_(x)=0`, so
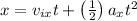`x=v_(i x) t+\left((1)/(2)\right) a_(x) t^(2)` for horizontal motion

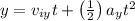`y=v_(i y) t+\left((1)/(2)\right) a_(y) t^(2)` for vertical motion

Given:

x = 35 m

`a_(x)=0 \mathrm{m} / \mathrm{s}^(2)`

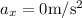
Need to find
`v_(i x)`

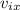
y = - 22 m

`v_(i y)=0 \mathrm{m} / \mathrm{s}`

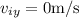
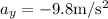`a_(y)=-9.8 \mathrm{m} / \mathrm{s}^(2)` (negative sign indicates downward motion)

By substituting all known values, we can solve for 't' value as below

`y=v_(i y) t+\left((1)/(2)\right) a_(y) t^(2)`

`-22=0(t)+\left(0.5 *-9.8 * t^(2)\right)`

`t^(2)=(-22)/(0.5 *-9.8)=(-22)/(-4.9)=4.4897`

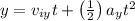
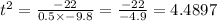
Taking square root, we get t = 2.12 seconds

Now, substitute these to find initial horizontal velocity

`x=v_(i x) t+\left((1)/(2)\right) a_(x) t^(2)`

`35=v_(i x)(2.12)+\left(0.5 * 0 *(2.12)^(2)\right)`

`35=v_(i x)(2.12)+0`

`v_(i x)=(35)/(2.12)=16.5 \mathrm{m} / \mathrm{s}`