Question

30 seconds of exposure to 115 dB sound can damage your hearing, but a much quieter 94 dB may begin to cause damage after 1 hour of continuous exposure. You are going to an outdoor concert, and you'll be standing near a speaker that emits 50 W of acoustic power as a spherical wave. What minimum distance should you be from the speaker to keep the sound intensity level below 94 dB?

Answer 1

39.8 m ≈ 40 m

Step-by-step explanation:

power (P) = 50 W

sound intensity level (
`p`) = 94 dB

the distance (r) can be gotten from the equation I =
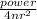`(power)/(4nr^(2) )` (take not that π is shown as
`n`)

making r the subject of the formula we have r =
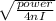`\sqrt{(power)/(4nI) }` (take not that π is shown as
`n`)

But to apply this equation we need to get the value of the intensity (I)

• we can get the intensity (I) from the formula sound intensity level (
  `p`) = 10 log₁₀
  `((I)/(I'))`

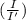
• rearranging the above formula we have intensity (I) =
  `I' x 10^{(p)/(10) }`

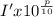
• I' = reference intensity = 1 x
  `10^(-12) W/m^(2)`

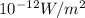
• now substituting all required values into the formula for intensity (I)

• I =
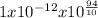  `1 x 10^(-12) x 10^{(94)/(10) }` = 0.00251
  `W/m^(2)`

now that we have the value of the intensity (I) we can substitute it into the formula for the distance (r)

distance (r) =
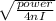
`\sqrt{(power)/(4nI) }`

r =
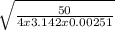`\sqrt{(50)/(4x3.142x0.00251) }` = 39.8 m ≈ 40 m