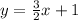Question

What is the equation, in slope-intercept form, of the line that is perpendicular to the line

y – 4 = –Two-thirds(x – 6) and passes through the point (−2, −2)?

Answer 1

`y=(3)/(2)x +1`

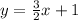
Explanation:

We are given;

The equation of a line;

`y-4 = -(2)/(3)(x-6)`

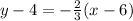
We are required to determine the equation of a line perpendicular to the above line and passing through (-2, -2).

• We can get the gradient of a line when given its gradient and a point where it is passing through.

• In this case;

We need to know that the product of gradient of two parallel lines is -1

• Therefore, we can get the gradient of the unknown line;

m₁× m₂ = -1

Thus;

m₂ = -1 ÷ -2/3

= 3/2

Thus, the gradient is 3/2 and the line passes through (-2,-2)

Thus, to get its equation, we take another point (x,y)

We get;

`(y+2)/(x+2)= (3)/(2)`

Then;

`2(y+2)=3(x+2\\2y + 4 = 3x + 6`

Combining the like terms,

`2y=3x+2`

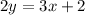
In the form of slope-intercept;

`y=(3)/(2)x +1`