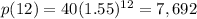Question

A moose population is growing exponentially following the pattern in the table shown below. Assuming that the pattern continues, what will be the population of moose after 12 years? Show all your work! Round your answer to the nearest whole number. (5 points)

Answer 1

The table referred to in the question is:

years=x population =y

0 40

1 62

2 96

3 149

4 231

Answer:

• 7,692 moose

Step-by-step explanation:

To discover the pattern followed by the data in the table, since it is indicated that the moose population is growing exponentially, you can find the multiplicative rate by dividing any two consecutive terms:

rate = 62/40 ≈ 96/62 ≈ 149/96 ≈ 231/149 ≈ 1.55

Thus, using the first ordered pair of the sequence, (0,40), you get the equation that models the exponential growing:

`p(x)=A_0(1.55)^(x)\\ \\ 40=A_0(1.55)^0\\ \\ 40=A_0* 1\\ \\ A_0=40\\ \\ p(x)=40(1.55)^x`

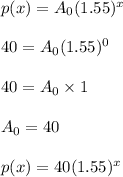
Then, to find the population of moose after 12 years, you substitute x = 12:

`p(12)=40(1.55)^(12)=7,692`