Question

Listed below are the amounts of weight change (in pounds) for 12 women during their first year of work after graduating from college. Positive values correspond to women who gained weight and negative values correspond to women who lost weight. Find the standard deviation for the given sample data. 1.0 -5 3.0 -8 14 -11 12 0 16 -2 12 7a. 1.0lbb. 8.1lbc. 2.0lbd. 3.0lb

Answer 1

`s= √(80.568)=8.97`

`Median =(1+3)/(2)=2`

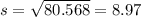
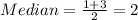
Explanation:

For this case we have the following data:

1.0 -5 3.0 -8 14 -11 12 0 16 -2 12 7

And ordering this data we have:

-11 -8 -5 -2 0 1 3 7 12 12 14 16

And we are interested in find the standard deviation for the sample data. In order to do this the first step is find the mean given by this formula:

`\bar X =(\sum_(i=1)^n X_i)/(n)=(1-5+3-8+14-11+12+0+16-2+12+7)/(12)=3.25`

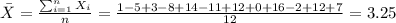
Now with the sample mean we can calculate the sample variance with the following formula:

`s^2 = (\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

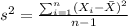
And if we replace we got:

`s^2 =80.568`

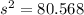
And for the sample deviation we just need to take the square root of the sample variance and we got:

`s= √(80.568)=8.97`

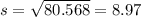
The median on this case would be given by:

`Median =(1+3)/(2)=2`

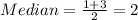
Using the positions 5 and 6 for the average since the sample size is an even number.