Question

15. Tell whether the lines for each pair of equations are parallel perpendicular or neither

Y=-3x+7
-2x+6y=3
16. Tell whether the lines for each pair of equations are parallel perpendicular or neither
Y=-1/5x+6
-2x+10y= 5

Answer 1

15. The lines are perpendicular.

16. The lines are neither perpendicular nor parallel.

Explanation:

15. The given lines are

Y=-3x+7 & -2x+6y=3 or, 6y = 3 + 2x or,
`y = 0.5 + (x)/(3)`.

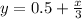The slope of the first line is -3 and the slope of the second line is
`(1)/(3)` [Comparing with the standard form of equation of straight line y = mx + c, where m is the slope of the straight line].

Two straight lines will said to be perpendicular to each other, if the product of its slopes will be equal to -1.

Since,
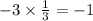`-3 * (1)/(3) = -1`, the equations are perpendicular with respect to each other.

16. The lines are
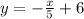`y = -(x)/(5) + 6` and -2x + 10y = 5 or, 10y = 5 + 2x or,
`y = 0.5 + (x)/(5)`.

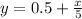As per the question number 15, it is clear that these equations are not perpendicular.

Here, the slope of the first one is
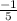`(-1)/(5)` and the slope of the second one is
`(1)/(5)`.

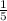The values are same with different sign. Hence, these equations are not parallel too.