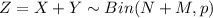Question

Let X and Y be independent binomial random variables having parameters(N,p) and (M,p), respectively. Let Z = X+Y;(a) Argue that Z has a binomial distribution with parameters(N+M,P) bywriting X and Y as appropriate sums of Bernoulli random variables.(b) Validate the result in (a) by evaluating the necessary convolution.

Answer 1

See explanation below.

Explanation:

Part a

For this case we can use the moment generating function for the bernoulli distribution for n trials, given by:

`p(s)^n = (q+ps)^n =\sum_(r=0)^n (nCr) (ps)^r q^(n-r)`

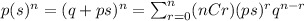
Wehre p is the probability of success and
`P(s_ = q+ps`

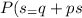
Using this property we see that;

If we multiply the two generating functions we got:

`p(s)^N = (q+ps)^N =\sum_(r=0)^N (NCr) (ps)^r q^(N-r)`

`p(s)^M = (q+ps)^M =\sum_(r=0)^M (MCr) (ps)^r q^(M-r)`

`p(s)^M p(s)^N = \sum_(r=0)^N (NCr) (ps)^r q^(N-r) \sum_(r=0)^M (MCr) (ps)^r q^(M-r)`

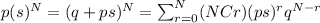
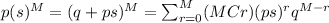
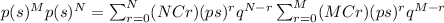
And the mass function would be given by:

`= (N+M C r) p^(r) (1-p)^(N+M-r)`

So we see that follows a binomial random variable with parameters (N+M, p)

Part b

For this case we are assuming that
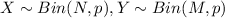`X \sim Bin (N,p) , Y\sim Bin (M,p)` and for this case we can assume that
`0 \leq k \leq N+M` for the proof.

We are interested on the random variable
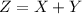`Z= X+Y` since the two random variables are independent we can write the probability mass function for Z like this:

`P(Z = X+Y = k) =\sum_(i=0)^k P(X=i , Y=k-i)`

`P(Z = X+Y = k) =\sum_(i=0)^k P(X=i) P(Y=k-i)`

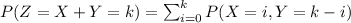
And we can replace the mass function for X and Y

`P(Z = X+Y = k) = \sum_(i=0)^k (NCi) p^i (1-p)^(N-i) \sum_(i=0)^k (M C i-1) p^(k-i) (1-p)^(M-K+i)`

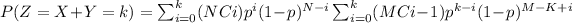
And we can rewrite this like that:

`P(Z = X+Y = k) = \sum_(i=0)^k (NCi) p^i (1-p)^(N-i) (M C i-1) p^(k-i) (1-p)^(M-K+i)`

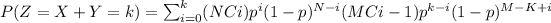
[We can take out the constant p:

`P(Z = X+Y = k) = p^k (1-p)^(N+M-k) \sum_(i=0)^k (NCi)(M C k-i)`

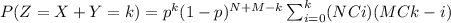
And using properties of the binomial formula we can write this like that:

`P(Z = X+Y = k) = (N+M Ck) p^k (1-p)^(N+M-k)`

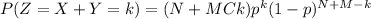
So then we see that
`Z= X+Y \sim Bin(N+M ,p)`