Answer:
The dimension of the rug would be 17 ft × 9 ft.
Explanation:
Given
length of the room = 27 ft.
width of the room = 19 ft.
suppose, she leaves a uniform strip of x ft. around the rug.
So,
The length of rug = (27-2x)ft.
Width of rug= (19-2x)ft.
∴ Area of the rug= length×width
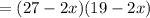
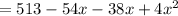
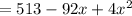
According to the question,

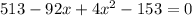 ( subtract 153 both sides)
( subtract 153 both sides)
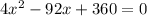
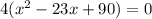
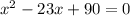
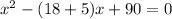 ( Middle term splitting)
( Middle term splitting)
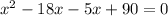
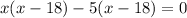
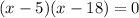
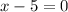 or
or
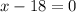 ( zero product property)
( zero product property)
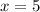 or
or
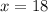
if x=18, dimension would be negative ( Not possible)
Thus, x= 5
Hence,
length of rug= 27-10=17 ft.
width of rug= 19-10=9 ft.