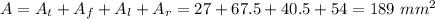Answer:
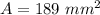
Explanation:
Surface Areas
Is the sum of all the lateral areas of a given solid. We need to compute the total surface area of the given prism. It has 5 sides, two of them are equal (top and bottom areas) and the rest are rectangles.
Computing the top and bottom areas. They form a right triangle whose legs are 4.5 mm and 6 mm. The area of both triangles is
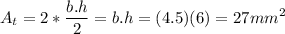
The front area is a rectangle of dimensions 7.7 mm and 9 mm, thus

The back left area is another rectangle of 4.5 mm by 9 mm
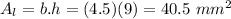
Finally, the back right area is a rectangle of 6 mm by 9 mm
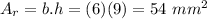
Thus, the total surface area of the prism is