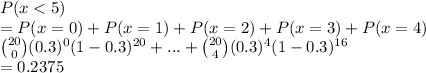Question

4-It has been a bad day for the market, with 70% of securities losing value. You are evaluating a portfolio of 20 securities and will assume a binomial distribution for the number of securities that lost value.

a- What assumptions are made when using this distribution.

b- Find the probability that all 20 securities lose value.

c- Find the probability that at least 15 of them lose value.

d- Find the probability that less than 5 of them gain value.

Answer 1

b) 0.0007

c) 0.4163

d) 0.2375

Explanation:

We are given the following:

We treat securities lose value as a success.

P(Security lose value) = 70% = 0.7

Then the securities lose value follows a binomial distribution, where

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

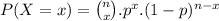
where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 20.

a) Assumptions

• There are 20 independent trials.
• Each trial have two possible outcome: security loose value or security does not lose value.
• The probability for success of each trial is same, p = 0.7

b) P(all 20 securities lose value)

We have to evaluate:

`P(x = 20)\\= \binom{20}{0}(0.7)^0(1-0.7)^(20)\\= 0.0007`

0.0007 is the probability that all 20 securities lose value.

c) P(at least 15 of them lose value.)

`P(x \geq 15)\\= P(x=15) + P(x = 16) + P(x=17) + P(x=18) +P(x = 19) +P(x = 20)\\ \binom{20}{15}(0.7)^(15)(1-0.7)^(5) +...+ \binom{20}{20}(0.7)^(20)(1-0.7)^(0) \\=0.4163`

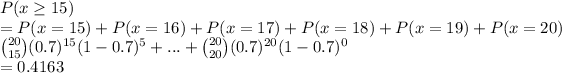
d) P(less than 5 of them gain value.)

P(gain value) = 1 - 0.7 = 0.3

`P(x < 5)\\= P(x=0) + P(x = 1) + P(x=2) + P(x=3) +P(x = 4)\\ \binom{20}{0}(0.3)^(0)(1-0.3)^(20) +...+ \binom{20}{4}(0.3)^(4)(1-0.3)^(16) \\=0.2375`