Question

If 4.05 g of KNO₃ reacts with sufficient sulfur (S₈) and carbon (C), how much P-V work will the gases do against an external pressure of 1.00 atm given the densities of nitrogen and carbon dioxide are 1.165 g/L and 1.830 g/L, respectively, at 20°C?

Answer 1

Step-by-step explanation:

Chemical reaction equation for the given reaction is as follows.

`2KNO_(3)(s) + (1)/(8)S_(8)(s) + 3C(s) \rightarrow K_(2)S(s) + N_(2)(g) 3CO_(2)(g)`

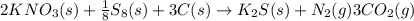
Therefore, we will calculate the number of moles of
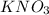`KNO_(3)` as follows.

No. of moles =
`\frac{mass}{\text{molar mass}}`

=
`(4.05 g)/(101.1 g/mol)`

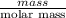
= 0.04 mol

Number of moles of nitrogen gas formed is calculated as follows.

No. of moles =
`(1)/(2) * \text{no. of moles of KNO_(3)}`

=
`(1)/(2) * 0.04 mol`

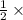
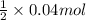
= 0.02 mol

Mass of
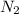`N_(2)` gas formed will be calculated as follows.

No. of moles × Molar mass of
`N_(2)`

=
`0.02 mol * 28.0 g/mol`

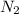
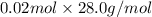
= 0.56 g

Now, the number of moles of
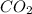`CO_(2)` formed is as follows.

=
`(3)/(2) * 0.04`

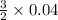
= 0.06 mol

Hence, mass of
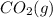`CO_(2)(g)` formed will be as follows.

`0.04 mol * 44 g/mol`

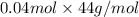
= 1.76 g

Volume of
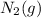`N_(2)(g)` is calculated as follows.

Volume =
`(mass)/(density)`

=
`(0.56 g)/(1.165 g/L)`

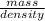
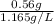
= 0.48 L

And, volume of
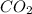`CO_(2)` is calculated as follows.

Volume =
`(mass)/(density)`

=
`(1.76 g)/(1.830 g/L)`

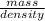
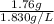
= 0.96 L

Let us assume that the volume of solids are negligible. Therefore, total volume will be as follows.

`\Delta V` = (0.48 L + 0.96 L)

= 1.44 L

Relation between work, pressure and volume is as follows.

w = -
`P_(ext) * \Delta V`

= -
`1.00 atm * 1.44 L`

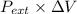
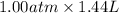
= -1.44 atm L

As 1 tm L = 101.3 J. So, convert 1.44 atm L into joules as follows.

`1.44 * 101.3 J`

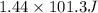
= 145.87 J

Thus, we can conclude that the given gases will do 145.87 J of work.