Question

9 cm

3 cm
AB is parallel to DC.
AD = 9 cm, DC = 3 cm. Angle BCD = 35°
Angle ABD = 90°
Calculate the size of angle BAD.
Give your answer correct to one decimal place.​

Answer 1

Explanation:

Answer 2

∴ ∠BAD =
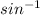`sin^(-1)`(0.2044) = 11.8°

Explanation:

i) AD = 9 cm

ii) DC = 3 cm

iii) ∠BCD = 35°

iv) Since AB is parallel to DC and ∠ABD = 90° then we can conclude that ∠BDC = 90°.

v)
`(BD)/(DC) = \frac{BD}{3\hspace{0.1cm}cm} = tan(35)` = 0.6128 ∴ BD = 3
`*` 0.6128 = 1.84 cm

vi) ∴ sin(∠ BAD ) =
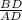`(BD)/(AD)` ⇒ sin(∠ BAD ) =
`(1.84)/(9)` = 0.2044

∴ ∠BAD =
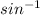`sin^(-1)`(0.2044) = 11.8°