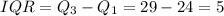Question

Suppose a biologist studying the mechanical limitations of growth among different species of tulips monitors a national preserve. He collects data on the heights of 10 different types of tulips in the reserve and rounds each height to the nearest centimeter.

25,21,26,24,29,33,29,25,19,24

Compute the first quartile (Q1), the third quartile (Q3), and the interquartile range (IQR) of the data set.

Answer 1

`Q_1 = 24`

`Q_3 = 29`

`IQR= Q_3 -Q_1 = 29-24 =5`

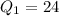
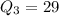
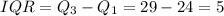
Explanation:

For this case we have the following dataset:

25,21,26,24,29,33,29,25,19,24

The first step is order the data on increasing order and we got:

19, 21, 24, 24, 25, 25, 26, 29, 29 , 33

For this case we have n=10 an even number of data values.

We can find the median on this case is the average between the 5 and 6 position from the data ordered:

`Median = (25+25)/(2)=25`

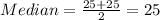
In order to find the first quartile we know that the lower half of the data is: {19, 21, 24, 24, 25}, and if we find the middle point for this interval we got 24 so this value would be the first quartile
`Q_1 = 24`

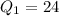
For the upper half of the data we have {25,26,29,29,33} and the middle value for this case is 29 and that represent the third quartile
`Q_3 = 29`

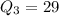
And finally since we have the quartiles we can find the interquartile rang with the following formula:

`IQR= Q_3 -Q_1 = 29-24 =5`