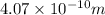Question

The second-order diffraction for a gold crystal is at an angle of 22.20o for X-rays of 154 pm. What is the spacing between the crystal planes?

Answer 1

Answer: The spacing between the crystal planes is
`4.07* 10^(-10)m`

Step-by-step explanation:

To calculate the spacing between the crystal planes, we use the equation given by Bragg, which is:

`n\lambda =2d\sin \theta`

where,

n = order of diffraction = 2

`\lambda` = wavelength of the light =
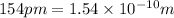`154pm=1.54* 10^(-10)m` (Conversion factor:
`1m=10^(12)pm` )

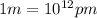d = spacing between the crystal planes = ?

`\theta` = angle of diffraction = 22.20°

Putting values in above equation, we get:

`2* 1.54* 10^(-10)=2d\sin (22.20)\\\\d=(2* 1.54* 10^(-10))/(2* \sin (22.20))\\\\d=4.07* 10^(-10)m`

Hence, the spacing between the crystal planes is
`4.07* 10^(-10)m`