Question

The length of a rectangle is 12 feet more than twice the width. If the area is 320 square feet, what is the length? What is the width?

Answer 1

• Length of rectangle is 32 feet and width is 10 feet

Step-by-step explanation:

Given,

• The length of a rectangle is 12 feet more than twice the width and area is 320 square feet

Let's assume, width of rectangle x feet and length of the Rectangle be 12 + 2x respectively. To Calculate the length and width of rectangle we'll use the formula of area of rectangle:

`\\ \star \: { \underline{ \boxed { \pmb{ \sf{ \purple{Area _((rectangle))= Length * width}}}}}} \\ \\`

Substituting the required values:

`\dashrightarrow \sf \: \: \: \: (12 +2x) (x) = 320 \\`

`\dashrightarrow \sf \: \: \: \: 12x + 2x^2 = 320 \\`

`\dashrightarrow \sf \: \: \: \: 12x + 2x^2- 320 = 0 \\`

`\dashrightarrow \sf \: \: \: \: 2x^2 + 12 - 320 = 0 \\`

`\dashrightarrow \sf \: \: \: \: 2(x^2 + 6x - 160) = 0 \\`

`\dashrightarrow \sf \: \: \: \: 2(x^2 + 16x - 10x - 160) = 0 \\`

`\dashrightarrow \sf \: \: \: \: 2(x - 10)(x + 16) = 0 \\`

`\dashrightarrow \: \: \: \: \underline{ \boxed{ \purple{ \pmb{ \rm{ x = 10 \: or \: -16}}}}} \\`

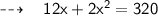
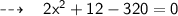
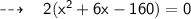
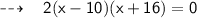
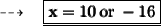
Hence,

• Width of rectangle = x = 10 feet
• Length of rectangle = 12 + 2x = 12 + 2(10) = 32 feet

`~`

`\underline{\therefore{ \pmb { \frak{Length \: and \: width \: of \: rectangle \: is \: 32 \: and \: 10 \:ft}}}}`