Question

A,B, and C are collinear, and B is between A and C. The ratio of AB to BC is 1:1

Answer 1

Therefore the coordinates of C is

C(4,9).

Explanation:

Given:

Point A , B , and C are Collinear.

i.e A-B-C is a Straight Line

AB : BC = 1 : 1

i.e B is the Mid Point of AC.

And Point A , B and C lie on the Same Line

point A( x₁ , y₁) ≡ ( 0 ,-9)

point B( x , y) ≡ (2 , 0)

To Find:

point C( x₂ , y₂) ≡ ?

Solution:

B is the Mid Point of AC. Hence by Mid point Formula,

`Mid\ point(AC)=((x_(1)+x_(2) )/(2), (y_(1)+y_(2) )/(2))`

Substituting the values we get

`B(2,0)=((0+x_(2) )/(2), (-9+y_(2) )/(2))`

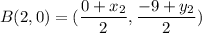
Substituting x and y value we get

`2=(0+x_(2) )/(2)\\and\\0=(-9+y_(2) )/(2)`

`x_(2)=4\\and\\y_(2)=9`

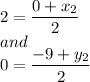
Therefore the coordinates of C is

C(4,9).