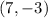The solution is
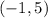 and
and
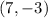
Explanation:
The expression is
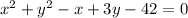 and
and
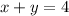
Using substitution method we can solve the expression.
Let us substitute
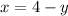 in
in
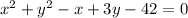
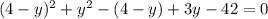
Expanding and simplifying the expression, we get,
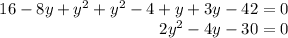
Let us use the quadratic equation formula to solve this equation,

Thus,
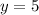 and
and
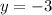
Substituting y-values in the equation
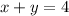 , we get the value of x.
, we get the value of x.
For
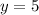 ⇒
⇒
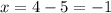
For
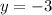 ⇒
⇒
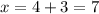
Thus, the solution set is
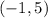 and
and