Question

The electric field everywhere on the surface of a thin, spherical shell of radius 0.770 m is of magnitude 860 N/C and points radially toward the center of the sphere.

(a) What is the net charge within the sphere's surface?
(b) What can you conclude about the nature and distribution of the charge inside the spherical shell?

Answer 1

(a)
`Q = 7.28* 10^(14)`

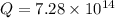
(b) The charge inside the shell is placed at the center of the sphere and negatively charged.

Step-by-step explanation:

Gauss’ Law can be used to determine the system.

`\int{\vec{E}} \, d\vec{a} = (Q_(enc))/(\epsilon_0)\\</p><p>E4\pi r^2 = (Q_(enc))/(\epsilon_0)\\</p><p>(860)4\pi(0.77)^2 = (Q_(enc))/(8.8* 10^(-12))\\</p><p>Q_enc = 7.28* 10^(14)`

This is the net charge inside the sphere which causes the Electric field at the surface of the shell. Since the E-field is constant over the shell, then this charge is at the center and negatively charged because the E-field is radially inward.

The negative charge at the center attracts the same amount of positive charge at the surface of the shell.