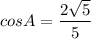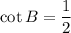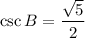Question

asked Jul 26, 2021 7.1k views

1 Answer

Angom · Answer 1 · 2021-08-01T21:24:06+0000

Answer:

Therefore,

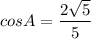
cos A=(2√(5))/(5)

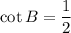
$\cot B =(1)/(2)$

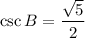
$\csc B = (√(5))/(2)$

Explanation:

Given:

Right △ABC has its right angle at C,

BC=4 , and AC=8 .

To Find:

Cos A = ?

Cot B = ?

Csc B = ?

Solution:

Right △ABC has its right angle at C, Then by Pythagoras theorem we have

$(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)$

Substituting the values we get

$(AB)^(2)=4^(2)+8^(2)=80\\AB=√(80)\\AB=4√(5)$

Now by Cosine identity

$\cos A = \frac{\textrm{side adjacent to angle A}}{Hypotenuse}\\$

Substituting the values we get

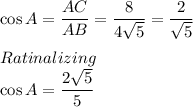
$\cos A = (AC)/(AB)=(8)/(4√(5))=(2)/(√(5))\\\\Ratinalizing\\\cos A=(2√(5))/(5)$

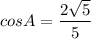
cos A=(2√(5))/(5)

Now by Cot identity

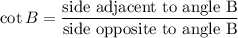
$\cot B = \frac{\textrm{side adjacent to angle B}}{\textrm{side opposite to angle B}}$

Substituting the values we get

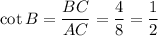
$\cot B = (BC)/(AC)=(4)/(8)=(1)/(2)$

Now by Cosec identity

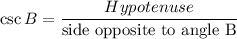
$\csc B = \frac{Hypotenuse}{\textrm{side opposite to angle B}}\\$

Substituting the values we get

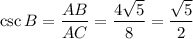
$\csc B = (AB)/(AC)=(4√(5))/(8)=(√(5))/(2)$

Therefore,

cos A=(2√(5))/(5)

$\cot B =(1)/(2)$

$\csc B = (√(5))/(2)$

Please log in or register to add a comment.