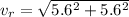Answer:
a)

b)
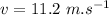
c)

Step-by-step explanation:
Given:
- diameter of bicycle-tyre,

- linear speed of tyre,
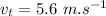
a)
angular speed of the tyre:
We know the relation between angular and linear speed as:
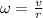
here
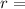 radius of the wheel
radius of the wheel
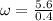

b)
Speed of blue dot on the periphery of the tyre when the dot is 0.8 meter above the ground:
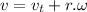
this velocity will be the sum of the linear velocity of the tyre and the tangential velocity of the point.
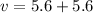
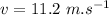
c)
When the dot is at a height of 0.4m it is either going down the rotation or it is going up the rotation which is normal to the linear velocity of the tyre, hence resultant effect is: